数学原来这么有用:游戏里的三角函数与运动轨迹
上课日期:2025年8月26日
上课时间:下午 1:55
上课时长:1小时 51分钟 32秒
一、这节课到底在学什么?
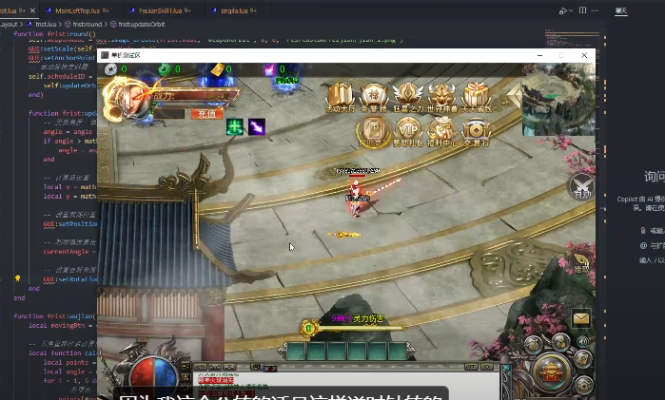
这节课的核心是学习如何在游戏开发中,运用基础的数学知识(特别是三角函数)来创建和控制物体的运动轨迹。例如,让一把剑围绕角色旋转,或者让一个物体沿着三角形、圆形、椭圆形的路径移动。老师通过通俗易懂的比喻和实战代码演示,让大家理解这些看似复杂的数学概念是如何在代码中变成具体效果的。
二、课程时间线梳理
-
开场-约27分钟:讲解了数学工具箱 (math) 的基本概念、角度与弧度的区别与转换(math.deg, math.rad),以及圆周率π (math.pi) 在计算圆周长、面积等实际问题中的应用。
-
约27分钟-1小时10分钟:详细讲解了三角函数。这是本节课的核心,包括:
- 正弦(sin)、余弦(cos)、正切(tan) 的定义(对边/斜边、邻边/斜边、对边/邻边)。
- 如何在Lua中正确使用
math.sin, math.cos, math.tan(必须传入弧度值)。
- 反三角函数 (
math.asin, math.acos, math.atan) 的作用(已知比例求角度)和使用规则(输出是弧度,需要注意取值范围)。
-
约1小时10分钟-1小时30分钟:讲解了向下取整函数 (math.floor) 和椭圆周长的计算方法。重点介绍了两种近似公式:简单的平均半径法和精度更高的雷伯恩公式,并解释了其应用场景。
-
约1小时30分钟-课程结束:实战演示。老师通过共享屏幕,现场演示了如何用代码实现物体沿等边三角形、圆形(包括公转和自转)、五角星和椭圆路径运动,将前面所讲的所有数学知识融会贯通。
三、重点知识点总结
-
数学工具箱 (math):把它想象成一个装满各种数学工具(如π、sin、cos)的箱子,用 math.工具名来使用它们。
-
角度与弧度:描述角大小的两种单位。180度 = π弧度 是转换基础。math.deg将弧度变角度,math.rad将角度变弧度。
-
三角函数定义:在直角三角形中,只要角度不变,三条边的比例就不变。
正弦(sin) = 对边 / 斜边余弦(cos) = 邻边 / 斜边正切(tan) = 对边 / 邻边
-
Lua中使用三角函数的关键:函数(如 math.sin(角度))括号里填的必须是弧度,不能直接写角度。常用写法是:math.sin(math.rad(30))。
-
反三角函数:知道两边比例,反推角度。输出结果是弧度,常需要再用 math.deg转为角度。
-
向下取整 (math.floor):直接舍去小数部分取整,不是四舍五入。(例如:math.floor(3.9)结果是 3)。
-
椭圆周长计算:需要长半轴(a)和短半轴(b)。
- 简单估算:周长 ≈ π * (a + b)
- 精确计算(雷伯恩公式):周长 ≈ π * [ 3(a + b) - √( (3a + b) * (a + 3b) ) ]
四、学完这节课你能掌握
- 理解原理:明白游戏里物体做圆形、椭圆形运动背后的数学逻辑,不再只是死记硬背代码。
- 使用工具:学会在Lua中正确调用
math库里的三角函数和常用函数,并理解角度和弧度的转换。
- 实现运动:能够借鉴课程中的实战代码,自己尝试编写让物体沿简单几何路径(如直线、圆形)运动的脚本。
- 解决问题:当需要实现复杂的运动轨迹(如飞剑环绕)时,知道其核心是数学计算,并有了进一步学习和查阅资料的方向。
课程评价
这节课的老师讲得非常出色。优点非常突出:
- 通俗易懂:老师全程使用“数学工具箱”、“站在楼梯上取整”等生活化比喻,将抽象的数学概念讲得生动形象,非常适合基础薄弱的学员。
- 逻辑清晰:课程从最基础的角度、弧度讲起,逐步深入到三角函数的定义、代码应用,最后进行实战演示,层层递进,结构合理。
- 注重互动与理解:老师频繁与学员“小文”互动,通过提问和举例确保关键概念被理解,强调“理解逻辑”而非“死记硬背”,这种教学方式非常有效。
- 理论结合实战:后半部分的代码实战演示非常宝贵,直观地展示了前面所有理论知识的实际应用,让学员看到了学习的目的和成果。
如果要说可以改进的地方,可能是课程后期实战部分节奏稍快,对于完全零基础的学员,可能需要反复观看回放或辅以更多注释才能完全消化。但总体而言,这是一堂准备充分、讲解耐心、内容扎实的优秀课程。
课程入口


 系统函数
系统函数